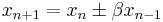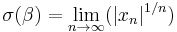Embree–Trefethen constant

In number theory, the Embree–Trefethen constant is a threshold value labelled β*.

For a fixed positive number β, consider the recurrence

$x_{n%2B1}=x_n \pm \beta x_{n-1} \,$

where the sign in the sum is chosen at random for each n independently with equal probabilities for "+" and "−".

It can be proven that for any choice of β, the limit

$\sigma(\beta) = \lim_{n \to \infty} (|x_n|^{1/n}) \,$

exists almost surely. In informal words, the sequence behaves exponentially with probability one, and σ(β) can be interpreted as its almost sure rate of exponential growth.

We have

σ < 1 for 0 < β < β* = 0.70258 approximately,

so solutions to this recurrence decay exponentially as n→∞ with probability 1, and

σ > 1 for β* < β,

so they grow exponentially.

Regarding values of σ, we have:

σ(1) = 1.13198824... (Viswanath's constant), and
σ(β*) = 1.

The constant is named after applied mathematicians Mark Embree and Lloyd N. Trefethen.

Literature

Embree, M.; Trefethen, L. N. (1999), "Growth and decay of random Fibonacci sequences", Proceedings of the Royal Society 455 (455): 2471–2485, doi:10.1098/rspa.1999.0412 [1]

External links

Weisstein, Eric W., "Random Fibonacci Sequence" from MathWorld.